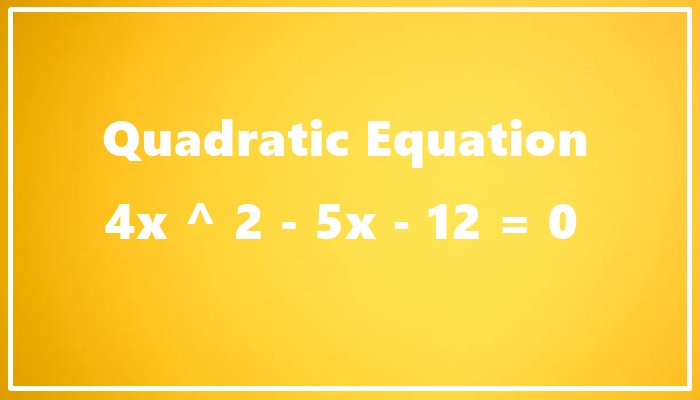Quadratic Equations, Also Referred To As Second-Degree Polynomial Equations, Are Usually Represented As Follows: Ax^2 + Bx + C = 0ax2+Bx+C=0 Ax2+Bx+C=0.. The Quadratic Equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 Will Be Solved In This Section. Within This Guide. Methodically, Applying A Variety Of Approaches.
Introduction To Quadratic Equations:
Definition And Standard Form:
A Second-Degree Polynomial Equation Of The Following Form Is Called A Quadratic Equation:
Ax^2 + Bx + C = 0ax2+Bx+C=0 Ax2+Bx+C=0
Where Xxx Is The Variable And Aaa, Bbb, And Ccc Are The Constants. The Equation In Our Instance Is 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0.
A=4a = 4a=4, B=−5b = -5b=−5, And C=−12c = -12c=−12 In This Case.
Techniques For Handling Quadratic Equations:
There Exist Multiple Techniques For Resolving Quadratic Equations:
1. Calculating
2. Making Use Of The Quadratic Formula
3. Finishing Up The Square
4. The Graphical Approach
For This Problem, The Quadratic Formula And The Factoring Method Will Be Our Main Concerns.
Factoring Technique:
The Quadratic Equation Is Rewritten Using The Factoring Method As The Product Of Two Binomials. We Search For Two Integers That Multiply To A⋅Ca \Cdot Ca⋅C (The Product Of The Coefficients Of X2x^2×2 And The Constant Term) And Add Up To Bbb (The Coefficient Of Xxx) For The Equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0.
Method By Method Factoring:
Recognize Ccc, Bbb, And Aaa:
A = 4, \Quad B = -5, \Quad C = -12, A=4, B = -5, C = -12
Determine A_Ca \Cdot Ca_C:
A \Cdot C = 4 \Cdot (-12) = -48a ⋅C = 4⋅(−12) = −48
Locate Two Values That Sum Up To -5-5-5−5 And Multiply By -48-48−48:
The Reasons These Are 333 And -16-16-16 Are As Follows: 3×(-16) = -483 \Times (-16) = -483×(-16) = -48 3+(-16) = -133 + (-16) = -133+(-16) = -13
Use These Values To Rewrite The Middle Term -5x-5x−5x:
4x^2 + 3x – 16x – 12 = 04×2 + 3x – 16x – 12 = 0
Sort The Terms:
(−16x−12) + (4×2+3x) = 0(4x^2 + 3x) + (-16x – 12) = 0(4×2 + 3x) + (−16x−12) = 0
Calculate The Phrases That Each Group Uses Frequently:
X(4x+3)−4(4x+3) = 0x(4x + 3) – X(4x + 3) = 0−4(4x + 3) = 0
Subtract The Common Binomial Coefficient:
(4x+3)(X-4) = 0(4 X + 3)(X – 4) = 0(4 X + 3)(X – 4) = 0
Solve For Xxx After Setting Each Element To Zero:
\Text{Or} \Quad X – 4 = 04x+3=0orx−4=0 \Quad 4x+3=0orx−4=04x + 3 = 0 X = 44x = −3orx=4 \Quad \Text{Or} \Quad X = 4x = −3orx=44 -\Frac{3}{4} \Quad \Text{Or} \Quad X = 4x=−43orx=4 X=−34orx=4
The Equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 Has These Answers As A Result. Are: X = -\Frac{3}{4} \Quad \Text{Or} \Quad X = 4x = −43orx=4; Thus,
Use Of The Quadratic Formula:
Any Quadratic Equation Of The Type Ax2+Bx+C=0ax^2 + Bx + C = 0ax2+Bx+C=0 Can Be Solved Using The Quadratic Formula, Which Is A General Technique. For Example, X=−B±B2−4ac2ax = \Frac{-B \Pm \Sqrt{B^2 – 4ac}}{2a}X=2a−B±B2−4ac
Method By Method With The Quadratic Formula:
Recognize Ccc, Bbb, And Aaa:
A = 4, \Quad B = -5, \Quad C = -12, A=4, B = -5, C = -12
Determine Δ\Deltaδ, The Discriminant:
Δ=B2−4acdelta Is Equal To B^2 – 4ac.Δ=B2−4ac Δ=(−5)2−4⋅4⋅(−12)\(-5)^2 – 4 \Cdot 4 \Cdot (-12) = Deltaδ=(−5)2−4⋅4⋅(−12) Δ=25+192\Delta Is Equal To 25 Plus 192.Δ=25+192 Δ=217\Delta = 217Δ = 217
Utilize The Formula For Quadratics:
X = -(-5) \Pm \Sqrt{217}}{2 \Cdot 4} = −(−5)±2172⋅4xx=5±2178x = \Frac{5 \Pm \Sqrt{217}}{8} X=2⋅4−(−5)±217x Equals 85±217
Make The Expression Simpler:
X=5+2178x = \Frac{5 + \Sqrt{217}}{8}X=85+217 X=5−2178x = \Frac{5 – \Sqrt{217}}{8}X=85−217 Are The Solutions.
Therefore, 04x^2 – 5x – 12 = 04×2 – 5x – 12 = 0 Is The Exact Solution To The Problem 4×2 – 5x – 12 The Following Are: X=5+2178orx=5−2178x = \Frac{5 + \Sqrt{217}}{8} \Quad \Text{Or} \Quad X = \Frac{5 – \Sqrt{217}}{8}X=85+217orx=85−217
Summary:
We Have Studied The Quadratic Equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 In This Guide. And Used The Quadratic Formula In Addition To The Factoring Method To Solve It. We Determined The Roots By Factoring, And They Are X=−34x = -\Frac{3}{4}X=−43 And X=4x = 4x=4. The Exact Roots, X=5+2178x = \Frac{5 + \Sqrt{217}}{8}X=85+217 And X=5−2178x = \Frac{5 – \Sqrt{217}}{8}X=85−217, Were Found Using The Quadratic Formula.
Comprehending These Techniques Offers A Solid Basis For Resolving Any Quadratic Equation.